31.05.2004
А.Шашин. ШАХМАТНЫЙ ПЛАН – ФИКЦИЯ ИЛИ РЕАЛЬНОСТЬ?
Я начинаю атаку. Мишень – шахматный план. Цель атаки – полномаcштабная дискредитация этого шахматного идола. Скажу коротко и совершенно определенно : в «новейшей» теории шахматной игры шахматному плану нет места! План – это фантом, призрак. Он – лишнее звено в цепочке рассуждений шахматиста при поиске сильнейшего хода. Шахматный план – это сказка для шахматных младенцев, сказка сомнительного достоинства....
Приступая к атаке, предупреждаю : я прекрасно вооружен и весьма «опасен». В моем арсенале – ультрасовременные методы науки третьего тысячелетия. В меру собственных сил я вооружен «идеологией» и «технологиями» научных теорий, претендующих на описание «всего на свете». Проблема лишь в выборе адекватного нашей мишени «абсолютного оружия».
По шахматному плану я «выстрелю» ... из тяжелых орудий победоносной теории динамических систем. Эта теория прекрасно зарекомендовала себя в «боях» со сложными системами в физике, химии, биологии, социологии и во многих других науках. Она же поможет и нам, поскольку шахматная игра имеет все признаки сложной системы (не буду перечислять). Теория динамических систем легко ассимилирует шахматную игру : модель игры будет создана по аналогии со стандартными моделями сложных систем в естествознании – систем, которые не знают слово «план»...
Неприятеля всегда целесообразно атаковать в его самом чувствительном, самом слабом месте. Поэтому моей первой, решительной и бескомпромиссной атакой будет атака на шахматный план в тех шахматных позициях, где доминируют иррациональные осложнения. В них о плане не может быть и речи : он там – нонсенс.
Затем, во второй и третьей частях статьи, ленивой и снисходительной атаке (скажу деликатнее : критике) будут подвергнуты шахматные планы уже в стратегически ясном миттельшпиле, а затем и в эндшпиле. Именно так. Но вначале...
Вначале иррациональные осложнения!
Почему?
Ответ : потому, что иррациональные осложнения и – добавлю – сопутствующие иррациональным осложнениям атаки материальных мишений всего ближе предстоят к истиной и неискаженной природе шахматной игры. Последняя же отождествляется мною с природой шахматного хаоса.
Хаос первичен. В шахматах же хаос – это бесконечное и первозданное множество всех возможных, то есть всех разрешенных правилами игры шахматных партий. Повторяю : всех шахматных партий без исключений. В том числе и бессмысленных партий!
Важно то, что хаос способен к самоупорядочению. Порядок вторичен. Добавлю : переход от хаоса к порядку происходит сам по себе, то есть спонтанно, происходит без внешнего воздействия на сложную динамическую систему. Работают внутренние параметры системы. Они – эти параметры – отвечают за «все без исключения»!
1.Иррациональные осложнения и атаки материальных мишеней.
Г.Каспаров – А.Карпов
Ленинград, 1986.
16-я партия матча на мировое первенство.

Вначале – сама партия (точнее сказать, ее финальный фрагмент) :
31.¢h2 ¦b3 32.¥d3 cd3 33.£f4 £a3 34.¤h6 £e7 35.¦g6 £e5 36.¦g8 ¢e7 37.d6 ¢e6 38.¦e8 ¢d5 39.¦e5 ¤e5 40.d7 ¦b8 41.¤f7 1:0
А затем – более чем целенаправленные комментарии (напоминаю : наша цель – дискредитация шахматного плана!).
Итак...
31.¢h2. Вероятно, сильнейшее продолжение атаки. Этим ходом :
а) Каспаров жертвует фигуру на а3 (впрочем, не видно, как ее спасти);
б) белые, «приподнимая» короля, увеличивают тем самым концентрацию своих сил на королевском фланге, поскольку «минимальный» прямоугольник f1-f4-h4-h1 (прямоугольник, внутри которого расположились семь белых фигур) после 31.¢h2 превратился в меньший по площади «минимальный» квадрат f2-f4-h4-h2;
в) Каспаров ходом в партии раз и навсегда избавляется от контригры противника, связанной с пренеприятнейшим шахом на с1.
Иначе говоря, Каспаров а) атакует, б) играет стратегически, в)ограничивает агрессивные возможности противника (профилактика, то есть та же защита!). В единый клубок переплелись все известные нам формы шахматной борьбы. На доске – преддверие хаоса!
32... cd3. Одно из четырех(!) возможных взятий.
33... £a3. По Каспарову – ошибка. Сильнее 33...d2, и далее (смотри варианты A и B) ... разверзлась бездна!
Чемпион мира начинает со скромной преамбулы : 33...d2 34.¤h6 ¤f6. И лишь затем...
А) 35.¦b3 £b3 36.£f6 £d5 37.¤f7 d1£ (37...¢e8 38.¤b1 d1£ 39.¤c3+-) 38.¤d6 ¢g8 39.£g6 ¢f8 40.£f6 ¢g8 41.¤f5 £f5 42.£f5 £d6 43.f4 £a3
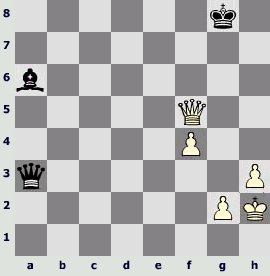
"Три пешки за фигуру дают белым здесь разве что моральный перевес" (Каспаров).
Оценка позиции чемпионом мира – оценка неопределенная, оценка «литературная» и весьма расплывчатая... Быть может, точнее будет ²/= ? Или ²?
Кто рискнет более точно оценить позицию на диаграмме, и как это сделать? Как? Ведь у нас реально есть лишь весьма и весьма скупой и ненадежный набор доступных нам средств : =,²,±... Где точные критерии оценки позиции? И есть ли они вообще?
B) 35.£d6 ¢e8 36.£c6 ¢f8 37.£d6 ¢e8 38.£a6 d1£ 39.£c8 ¢e7 40.£c5 ¢d7 41.£c6 ¢e7 42.d6 ¢f8 43.£c8 ¢g7 44.¤f5 ¢h7 45.£f8 ¤g4 46.¦g4 ¦h3 47.¢h3 £h1 48.¢g3 £e5 49.¦f4 g5 50.£f7 ¢h8 51.£f8 ¢h7 52.£e7 £e7 53.de7 gf4 54.¢f4 £g2 55.e8££g4 56.¢e5 £e4 57.¢e4 – пат!
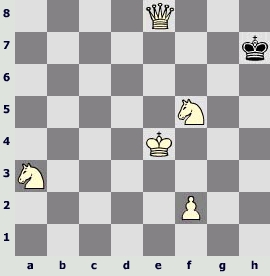
По моим самым осторожным арифметическим подсчетам, позиция на диаграмме – это всего лишь одна «реальная» шахматная позиция из... десятков тысяч возможных и несостоявшихся финальных шахматных позиций. Тех позиций, в которых шахматист прерывает расчет вариантов и приступает к оценке ситуации на доске. Одна точная позиция на сотни, тысячи позиций неточных!
...В только что приведенных мною красивых вариантах воедино переплелись и атака, и контратака противника (с точки зрения белых – защита) , и стратегическая игра. Все вместе они определяют, так называемый, перемешивающий слой – центральное понятие теории динамических систем. В перемешивающем слое царит хаос, господствуют неопределенность и Его Величество Случай. При этом нам – шахматистам – необходимо абсолютно точно осознать прозрачную истину : Его Величество Случай – это не результат нашей с вами некомпетентности или недобросовестности. Он – Его Величество Случай – есть всего лишь символ нашего истинного незнания, символ принципиальной невозможности абсолютно точно оценить шахматную позицию. Порядок в шахматах – это островки знания в океане хаоса. Мы обречены блуждать в дебрях шахматных вариантов. Шахматы – практически неисчерпаемая игра.
А теперь – о плане. Шахматный план в хаотических позициях (иррациональные осложнения!) – это нонсенс. Именно так, поскольку шахматист теряет контроль над шахматной стихией. Мы не знаем, что нас ждет впереди: нельзя объять необъятное. Мы – шахматисты, – выбирая тот или иной ход из множества кажущихся нам разумных ходов, не знаем наперед – где ошибка, а где, быть может, божественный импульс гениальности. Никаким самым добросовестным анализом такие позиции (я возвращаюсь к разбираемой нами партии двух чемпионов мира) не исчерпать. Можно лишь бесконечно долго приближаться к недостижимой истине. Бесконечно!
34.¤h6 . Грозит мат на f7.
35.¦g6. Снова грозит мат, но уже на поле g8.
36.¦g8. Шах – открытое нападение на короля!
37.d6. Еще один шах.
38.¦e8. Сплошные шахи! Почему все так просто?
39.¦e5. Решающий исход борьбы выигрыш материала и ... снова шах!
Правильно атаковать (в том числе и атаковать в иррациональных шахматных позициях) – это значит атаковать в соответствии с иерархическим шахматным рядом. Вот он, этот хорошо известный всем шахматистам ряд : король, ферзь, ладья, слон или конь, пешка... Главная мишень – король! В этом-то, то есть в следовании иерархическому шахматному ряду, и состоит весь нехитрый «план» при атаке. Добавлю к вышесказанному, добавлю, опираясь на азбучные истины теории динамических систем: чем дальше отстоит система от тупого состояния термодинамического равновесия, то есть чем больше ее неустойчивость, тем уже горизонт возможных предсказаний (планирования) ее будущего.
«Планы» на один-два хода вперед?
...Еще один, второй по счету и не менее поучительный пример: фрагмент одной из самых лучших партий чемпиона мира по версии ФИДЕ.
А.Халифман – П.Леко
Линарес, 2000.

Позиция на диаграмме возникла после хода белых 20.¦f1 – хода, хорошо известного знатокам этого острого варианта защиты Грюнфенда. Далее было (обойдемся пока без комментариев) :
20...¥f8 21.d7 £a2 22.¥b5 a6 23.¥a4 ¤f3 24.¢g2 ¤e5 25.¥b6 £c4 26.£d4 £d4 27.¥d4 ¤d3 28.¥c6 ¤c5 29.¦c7 ¥d6 30.¥c5 ¥c7 31.¥a8 ¦a8 32.¥e7 ¦d8 33.¦d1 f5 34.¥d8 ¥d8 35.ef5 gf5 36.¦d6 ¢f7 37.¦a6,
и белые, продемонстрировав отличную эндшпильную технику, выиграли партию на 47-м ходу (1:0).
А теперь – мои специальные, «предельные» и узконаправленные комментарии (наша цель остается неизменной – шахматный план!). Очередная дискредитация его гарантирована!
20...¥f8. Альтернатива ходу в партии – ход 20...¦d7. Чемпион мира продолжает этот вариант пока без комментариев : 21.¦d7 ¤d7 22.f4 , а затем переходит к анализу ... пяти(!!) его полноценных разветвлений. Вот они : 22...¦d8, 22...£d4, 22...g5, 22....¦c8 и 22...e5. 5 из 47 возможных ходов черных! Коэффициент хаотичности – 5/47 или 11%.
21...£a2. Возможно 21...¦db8.
22.¥b5. Встречалось и 22.¦e1...(Крамник – Каспаров, Линарес,1998).
22...a6. Анализу подвергнуто также и продолжение 22...¥g7.
23.¥a4. Возможно 23.f4.
23...¤f3. Халифман анализирует также еще два продолжения: 23...¤c4 и 23...£a3. В последнем из них – 23...£a3 – возможные ответы белых – это ходы 24.f4, 24.¥b6 и 24.¢g2. Все они проанализированы победителем весьма и весьма подробно. Варианты с разветвлениями!
24...¤e5. Преддверие апофеоза воистину титанической работы. Халифман свидетельствует о многолетних (1984-1989гг) и почти забытых им анализах. При этом, что удивительно даже для него, докомпьютерные, то есть на 100% «белковые» шахматные анализы оказались анализами высококачественными. Компьютерная правка в марте 2000-го года была минимальной!
Тщательнейшему исследованию был подвергнут коварный шах конем – 24...¤h4.
Немыслима даже попытка перепроверить все эти чудовищные по объему анализы – столь они пространны. Судите сами : перед вами – один из ... трехзначного(!!!) числа опубликованных чемпионом мира вариантов. Речь идет о варианте, «обслуживающем» 24...¤e5 – ход в партии. Варианте с порядковым номером ... B4b22322 (впечатляет, не правда ли?). Вот он : 24...¤h4 25.¢h1 £c4 26.f3 g5 27.¥b6 ¥d6 28.¦f2 ¥e5 29.£c2 £b4 30.¦f1 £e7 31.¥d8 ¦d8 32.¦b3 £f6 33.£e2 £f4 34.¦b4 ¢g7 35.¦c4±.

Варианты причудливо расходятся в тех «точках» шахматных траекторий, которые соответствуют ходам 25.¢h1, 26.f3, 26... g5, 27.¥b6, 30.¦f1, 31... ¦d8, 34.¦b4 и 34...¢g7. Такие процессы в физике называются процессами бифуркационными : варианты «раздваиваются», затем «раздваиваются» варианты вариантов и т.д.
И вновь – мои соболезнования любителям игры по плану. Повторяю (см. также примечания к предыдущей партии) : позиция на диаграмме – это всего лишь одна «реальная» шахматная позиция из десятков тысяч возможных и несостоявшихся финальных шахматных позиций. Ее оценка (оценивает чемпион мира!) – ±.
Где точные весы?
У человека их нет. Точно «взвешивает» позицию только компьютер (очень спорное утверждение!). Однако, бесспорно то, что компьютер (конечно, не сам он, а авторы программы) не «боится» это делать...
25.¥b6. По крайней мере, – восемь разветвлений (восемь точек бифуркаций).
25...£c4. Немыслимо большое количество проанализированных разветвлений! Легко обнаружить варианты типа ... B7a222. Воистину титанический анализ!
26.£d4. И только после этого мощного хода белых общее число заслуживающих внимания вариантов идет на убыль. И это неспроста, поскольку Халифман оценивает позицию после 26.£d4, как позицию технически выигранную.
28...¤c5. Один из последних всплесков аналитической активности чемпиона мира. Анализу подвергнуты варианты 28...e5, 28...¤b4, 28...¥g7, 28...¥d6 и 28...¥c5. Всего – пять продолжений! Коэффициент хаотичности позиции – 5/30, то есть 17%. Проверьте!
29...¥d6. Возможно 29...¦ab8... +- .
31...¦a8. Или 31...¦d7 32.¥e3 +-.
32...¦d8. Проигрывает и 32...f6.
33...f5. Не спасает и 33...a5.
37.¦a6 (см. диаграмму).

Белые выиграли.
...Третьего примера на тему иррациональных осложнений и атак материальных мишеней не будет. Довольно! Я сделаю лучше вот что : добросовестно соберу воедино все самое ценное для нас – важнейшие понятия и определения, которые были бессистемно разбросаны по всей статье. А затем все это я дополню двумя - тремя азбучными истинами современной науки...
Итог – четыре тезиса (см. ниже). Они – основа «идеологии» проповедываемой мною «новейшей» теории шахматной игры. Внимание!
1. Модель шахматной игры станет динамической моделью тогда, когда мы догадаемся «впрыснуть» в модель хорошо известный науке принцип «lineaminorisresistentiae» (принцип «линии наименьшего сопротивления»). Отмечу тот факт, что этот важнейший для любой солидной теории принцип ввел в теорию шахматной игры еще Эм. Ласкер – второй чемпион мира по шахматам.
2. Шахматный хаос первичен. Он представляет собой бесконечное множество всех возможных шахматных партий. Или иначе : шахматный хаос – это совокупность всех без исключений шахматных «траекторий» (шахматное дерево). Физический аналог – термодинамические хаотические системы в Природе. «Законы» - правила шахматной игры.
Важнейший нюанс : ценности всех без исключений шахматных фигур равны нулю. В том числе – короля!
3. Постулируя бесконечную шахматную ценность короля, мы мгновенно частично упорядочим шахматную систему. Возникнет собственно шахматная игра (цель игры – мат неприятельскому королю). Для нас важно то, что при переходе от хаотической шахматной игры к игре частично упорядоченной элементы хаоса в системе останутся. Они – эти элементы хаоса – неуничтожимы.
4. Динамической системе, если она достаточно сложна, не нужен «надзиратель». Система сама «принимает» решения. «Принимает» решения случайным образом.
Где и когда?
В точках бифуркаций при «скольжении» сложной динамической системы вдоль «линии наименьшего сопротивления»!
Часть II.
Дискредитируя шахматный план, мы дискредитируем тем самым и теорию позиционной игры Вильгельма Стейница. Все обстоит именно так, а не иначе, поскольку шахматный план является одним из столпов этой теории.
Эпоха безраздельного господства над умами шахматистов более чем вековой «идеологии» Вильгельма Стейница завершается. Теория Стейница (лучше будет сказать, не теория, а некая предтеория, то есть предтеча «истинной» и грядущей теории шахматной игры) потеряла свою пробивную силу. Она иссякла и устала. Теория не отвечает современным критериям научности : Стейниц противоречив и бесконечно далек от математики.
Почему? Или : в чем первопричина ее – теории Стейница – несоответствия современным реалиям шахматной игры?
Отвечу коротко и недвусмысленно : шахматная игра не вмещается в узкое для нее ложе классических научных представлений. Добавлю : при описании нами шахматной системы нам будет необходимо дополнить традиционную двузначную логику, с ее классическими «да» и «нет», новой, третьей по счету логической валентностью!
...Первый чемпион мира по шахматам создал свою теорию в эпоху абсолютной гегемонии в науке классических представлений. Физика Ньютона объясняла в те, не знающие никаких сомнений наивные времена практически «все на свете». Ничтожные проблемы где-то на периферии науки (теория излучения, электродинамика...) считались проблемами временными и легко преодолимыми. В науке и в общественной жизни царили неподдельный оптимизм и вера в незыблемость установившегося миропорядка.
Стейниц умер на рубеже столетий – в 1900-м году. Он не застал двадцатый век – век революционных потрясений, двух мировых войн и ... тяжелейшего кризиса оснований фундаментальных наук – математики и физики в первую очередь. В тридцатые годы двадцатого столетия математикам пришлось отказаться от иллюзии всемогущества обожествленного ими формально-логического подхода (тяжелейшая травма!); физикам – в это же время – от «абсолютных» истин теории Ньютона. Методами самой математики было строго доказано, что математику, как науку, нельзя полностью «вывести» из какой-либо непротиворечивой формально-логической системы. Система может быть любой степени сложности : математика «не вмещается». Физикам же пришлось, находясь под давлением неожиданной для них лавины экспериментальных фактов, ввести в физическую науку принцип неопределенности. Этот принцип стал фундаментальным принципом современной физики : абсолютно точные измерения физических величин невозможны!
И тогда прежде предельно ясная – «да» или «нет» - двузначная ньютонова картина окружающего нас мира рухнула. В одночасье она стала картиной туманной, неопределенной. Истина ускользнула; она нашла надежное убежище в хаосе. Картина мира стала многозначной, «бифуркационной» (см. тезисы в конце первой части статьи). Вот тогда-то физики и стали поклоняться Его Величеству Случаю.
Резюме : грядет «истинная» теория шахматной игры...
2.Стратегический миттельшпиль
Начну с ошеломляющего примера – шедевр Найджела Шорта!
Н.Шорт – Я.Тимман
Тилбург, 1991.

Белые выиграли партию марш-броском короля к полю g7!
32.¢g3 ¦ce8 33.¢f4 ¥c8 34.¢g5 1:0
После 34...¥d7 35.¢h6 мат неизбежен.
Что сказать?
Великолепно!
Возможно, однако, что шедевру Найджела Шорта не уступает по своей красоте шедевр Акибы Рубинштейна (см. диаграмму). Впрочем, судите сами...
А.Рубинштейн – Е.Боголюбов
Вена, 1922.

Здесь белые сыграли...
22.g3
Слово Ю.Разуваеву и В.Мурахвери – авторам книги о выдающемся польском шахматисте : «В таких ходах ощущается суперкласс! Умение успеть сделать все полезные ходы до форсированных операций значительно упрощает реализацию преимущества. Наличие «форточки» чрезвычайно важно при вскрытии игры».
А теперь несколько слов от себя...
Как известно, фактор шахматной безопасности короля есть всего лишь... один из двузначного числа общепринятых признаков шахматной позиции по Стейницу. Повторяю: двузначного! Поэтому мы, играя партию, не в состоянии все время надежно контролировать такое неподъемное для нас «богатство». Как правило, мы – шахматисты – при оценке позиции во время партии надежно контролируем только один, доминирующий в исследуемой позиции шахматный признак. Какой именно – подсказывает опыт, интуиция. Четкого алгоритма (эвристики!) поиска сильнейшего хода у нас нет.
Еще одно : проблему поиска сильнейшего хода во время партии усугубляет и тот тревожный факт, что большая часть шахматных признаков позиции определена теорией Стейница неточно. Мы, на что я уже успел посетовать, бесконечно далеки от математики...
Ход черных. Боголюбов ответил
22...¦dc8
Черным совсем плохо. Если 22...¥c6, то 23.¦5c6 с гарантированным уничтожением ферзевого фланга неприятеля.
23.¤b8 ¦b8 24.¥b5 ¥d8
"24...ab5 было бы фатально ввиду 25.£a7" (С.Тартаковер).
25.¥e8
Атака материальной мишени.
Это мы уже «проходили» - см. первую часть статьи.

25...£f8
Или 25...¥c7 26.£c7 £c7 27.¦c7+-.
26.¦b7
Выигрывает немедленно.
26...¥a5 27.¦b8 £d6 28.¦b7 ¥b6 29.¦c6 £b4 30.¥f7
1 : 0
Одна из самых замечательных партий Рубинштейна...
Наивный вопрос (напоминаю : цель статьи – полномасштабная дискредитация шахматного плана) : шахматный план, где ты?
В этой партии я его не вижу. Близоруко прищурясь, я вижу разве что остроумную тактическую перепалку, которую белые предварили одним – единственным тихим ходом – ходом страшной силы – победоносным 22.g3. Этим ходом Рубинштейн ... приподнял – и это я вижу совершенно отчетливо! – свою пешку. Приподнял ее на одну вертикаль вверх. Иными словами, Рубинштейн сместил вертикально вверх центр тяжести собственной позиции. Смещение – к полям пешечных превращений, и оно минимально!
Вопрос : не прячется ли за спиной этого элементарного акта пространственной шахматной экспансии истинная природа стратегической (позиционной) игры?
...Иду далее (простите, шаг назад) : вернемся к фрагменту партии Шорта. Вопрос по аналогии : не является ли атака жизненно важного для черных поля g7 (марш-бросок ¢h2 – h6!) проявлением все той же сути шахматной игры? Белые, если нам удастся избавиться от мешающих рассудку эмоций ... приподнимают короля!
Да или нет?
Да!
Добавлю : экспансия ... предопределена! Действительно, правилами шахматной игры предусмотрены перемещения пешек только по вертикали вверх, всегда в одном направлении. За пешками, поддерживая их, следуют фигуры...
М.Ботвинник – В.Ненароков
СССР,1933.

26.a3
Удивительно! Ботвинник самым «бессмысленным» образом (у пешки нет шансов стать ферзем и, кроме того, после хода в партии она ни на йоту не приблизилась к полю превращения) приподнимает свою самую ничтожную пешку. Пешка приподнимается как бы инстинктивно, в силу инерции маховика военной машины, приподнимается на фоне тотального подтягивания всех резервов к линии фронта.
26...¢d7 27.£e2
Белые не торопятся.
27...¦b8 28.£d3 ¢e8 29.¥d1 ¤g6
Лучше 29...¥d7, не допуская активизации слона противника.
30.¥a4 ¢f8 31.¢f3
Молох тотальной экспансии неумолим.
31...¢g8 32.£d4
Последние приготовления.
32...¦f8

33.¤f5
Победоносное, тщательно подготовленное вторжение на территорию противника. Успех обеспечен, поскольку у белых налицо превосходство над противником не только по фактору шахматного времени, но и по фактору компактности их позиции. А именно : у белых больше и подвижность их фигур, и плотность упаковки (та же концентрация) их сил на участке атаки.
33...¥f5 34.ef5 ¤e7 35.¥d7
Слон торопится на поле e6.
35...¦h7 36.fg5 fg5
«Или 36...£g5 37.¦h5 £g7 38.g5 c5 (38..fg5 39.¥e6 ¢h8 40.¦h6) 39.¥e6 ¢h8 40.gh6 £g3 41.¢g3 cd4 42.cd4 ¤c6 43.¦5h4 и т.д.»(Ботвинник).
37.¥e6 ¦f7
Если 37...¢h8, то 38.¦h6 с победой.
1 : 0
После 38.£g7 ¢g7 39.¥f7 ¢f7 40.¦h6 сопротивление бессмысленно.
Победа Ботвинника – образец медленной, осторожной и как бы ползучей экспансии в стратегическом миттельшпиле. Экспансия – ключ к успеху в стратегически лучших позициях? Или, быть может, экспансия есть то нечто драгоценное для нас, что мы впоследствии рискнем возвести в ранг универсального стратегического плана?
Интуиция, взлелеянная многолетним опытом, подсказывает: «да!», «да!» и еще раз «да!». Интуиция выше логики, выше разума...
Объяснения («объясняем» вдохновение?!) еще будут. Я, право же, смущен, но я и ... обречен. Я обречен на то, чтобы продолжить свои «объяснения». Они будут неизбежны до тех пор, пока игнорируемая нами математика не будет нами же востребована. Без математики мы – шахматисты – обречены на малоэффективную «словесность» (жесткая терминология Михаила Ивановича Чигорина!).
Особое внимание прошу обратить на комментарии к 42-му ходу белых в последней, четвертой по счету партии в этой части статьи – блестящая победа Анатолия Карпова! Комментарии к партии, как, в неменьшей степени, и пространный постскриптум к ней, вплотную приблизят нас к долгожданной цели. Дискредитация шахматного плана подведет нас к мысли о неизбежности краха этого идола – идола, восходящего к эпохе Вильгельма Стейница.
Заменим идол Стейница «новейшим» шахматным идолом!
Да будет так. Аминь.
А.Карпов – В.Унцикер
Ницца, 1974, олимпиада.

37.¦a3
Вероятно, что в план белых (план или все-таки «план»?) входит почти очевидное 38.¦1a2 с последующим разменом белопольных слонов + £a1 и ¥b6(¥e3). После этого – размен одной пары ладей + победоносное вторжение двух, оставшихся после размена ладей, тяжелых фигур по вертикали «a». Не зря же Карпов приподнимает ладью! Место для ферзя – поле a1.
37...¢f8 38.¦1a2
Я – пророк?
38...¢g8
Черным остается только одно – ждать.
39.¤g4
Этот ход можно считать невинным и непринципиальным уточнением к продекларированному нами плану (плану или «плану»?). Карпов не торопится : конь на e3 расположен значительно лучше.
39...¢f8
Плохо 39...¥h5 40.¤h5 £h5. Отрезвляет41.¤f6.
40.¤e3 ¢g8 41.¥f7
Все по плану?
41...¤f7

42.£h5
Гром небесный!
Воистину удивительный ход, ставящий в тупик легионы добросовестных «классических» комментаторов! Почему, спрашивается, белые неожиданно вторгаются ферзем на поле h5, а не отводят его на заранее подготовленное маневрами ладей поле a1? Или, если вдруг наивнейшим образом предположить, что вторжение на h5 было запланировано Карповым еще на 37-м ходу или даже раньше, то, спрашивается, зачем тогда белым понадобились явно лишние для этой акции ходы 37.¦a3 и 38.¦1a2? Зачем?
...Еще Капабланка отметил тот факт (кто сделал это раньше его?), что в стратегически лучших позициях сильнейшей стороне целесообразно не спешить с началом активных операций. Психологическая подоплека этого практически ценного совета очевидна : с каждым ходом увеличивается вероятность ошибки слабейшей стороны (защищаться труднее, чем атаковать!?).
Вопрос : нет ли здесь, кроме психологической еще и чисто шахматной, объективной подоплеки?
Пожалуй, она есть. Или даже : разумеется, есть! Она реальна, поскольку, как мы это прекрасно знаем, объективно существуют такие шахматные позиции, где фактор шахматного времени не имеет решающего значения. И если все действительно обстоит именно так, а не по иному, то тогда нам было бы вполне уместно задать себе еще один, новый и бесхитростный вопрос : нельзя ли потратить сильнейшей стороне это «лишнее» шахматное время на «бесплатное» усиление собственной позиции?
Ответ очевиден : да! Но как это сделать практически?
Трезво поразмыслив мы приходим к выводу о необходимости (целесообразности!?) усиления позиции (изменения ее!?) за счет именно экспансии. Действительно, приподнимая позицию и ничем не рискуя при этом, мы тем самым реально увеличиваем свои шансы на успех : в грядущей тактической стычке у нас будут задействованы все фигуры и пешки, поскольку все наши силы будут заблаговременно подтянуты к линии фронта!
Вернемся однако к партии ...
42...¤d8
Или 42...¤h8 43.¤g4 £h5 44.¤h5 ¢f7 45.¥b6 ¦a3 46.¦a3 ¦a8 47.¦a8 ¤a8 48.¥d8 или 48.¥a5 с победой (по Карпову).
43.£g6 ¢f8 44.¤h5

Благоговейный ужас!
После 44...£g6 45.fg6 и 46.¤f5 (кто мог заранее предположить такую метаморфозу?) белые выигрывают немедленно...
А теперь (внимание: очень важно!) я убедительно прошу вас, уважаемый читатель, сравнить позицию после 45.fg6 с множеством потенциально возможных шахматных позиций после «запланированных» 42.£a1, 43.¥b6 и т.д.
День и ночь! Два абсолютно непохожих один на другой шахматных сценариев! Не правда ли?
Ответ однозначен: да! Добавлю: мы – свидетели ... шахматной точки бифуркации, свидетели «раздвоения» шахматных планов. Система «принимает» решение случайным образом. Каисса – богиня шахматной игры – играет в кости: выпало 42.£h5, а не 42.£a1. Его Величество Случай – верный раб божий? Да или нет?
Ускользающая от тесных объятий развращенного двузначной логикой разума шахматная истина находит надежное убежище в недрах неопределенности...
Третья логическая валентность?
1 : 0
...Обещанный постскриптум. Я его преподам вам в виде тезисов (см. также тезисы в конце первой части статьи). Тезисов – всего пять . Пять шагов к цели. Внимание!
1. Его Величество Случай (предположим, что мы находимся «внутри» хаотической шахматной системы) самым причудливым образом перемешивает шахматный материал. Начальная шахматная позиция постепенно «расползается» по всей плоскости шахматной доски. При этом собственно шахматные фигуры, то есть белые и черные короли, ферзи, ладьи, слоны и кони, распределяются по шахматной доске более или менее равномерно. Пешки же, в силу специфики своей шахматной природы, концентрируются вблизи полей шахматных превращений.
Иными словами, пространственная шахматная экспансия закреплена правилами игры на «генетическом» шахматном уровне.
2. При переходе от хаотической шахматной игры к игре частично упорядоченной (цель игры – мат неприятельскому королю) экспансия становится целенаправленной. Она ускоряется. Причина ускорения – благоприобретенная «материальная заинтересованность».
Фигуры сильнейшей стороны проникают на территорию противника и атакуют материальные мишени и стратегически ценные пустые шахматные поля. Пешки «ускоряются», поскольку они мечтают стать ферзями!
Пространственная шахматная экспансия становится тотальным фактором шахматной игры при атаке.
3. Не только фигуры и пешки, но и пустые шахматные поля обладают ненулевой шахматной ценностью. Пустые шахматные поля суть полноценные участники бифуркационного процесса.
4. Среднестатистическая шахматная ценность пустых шахматных полей меньше (много меньше) шахматной ценности фигур. Поэтому интенсивность взаимодействия пустых полей с полями, занятыми фигурами, меньше (много меньше) интенсивности взаимодействий фигур с фигурами.
Стратегическая игра – это игра, где доминируют взаимодействия фигур с пустыми полями. В игре же комбинационной доминируют взаимодействия фигур с фигурами. Поэтому частота появлений точек бифуркаций при «скольжении» шахматной системы вдоль «линии наименьшего сопративления» в стратегически определившихся позициях мала. Отсюда – соблазн долгосрочного планирования.
5. Шахматный план (в смысле Стейница) есть всего лишь фрагмент более гибкой теоретической конструкции. Стейниц прекрасно «работает» там, где нет точек бифуркаций. Там, где они есть, Стейниц бессилен.
Продолжение следует...
Использованная литература :
Часть I.
1) Г.К.Каспаров «Два матча». Москва, «Физкультура и спорт», 1987.
2) Александр Халифман «История старой тетради». «Шахматный Петербург» N2(16), 2000.
3) Д.С.Чернавский «Синергетика и информация». Москва, «Наука», 2001.
Часть II.
1) Ю.С.Разуваев, В.И.Мурахвери «Акиба Рубинштейн». Москва, «Физкультура и спорт»,1980.
2) А.Шашин «Стратегический миттельшпиль». «Шахматный Петербург» N2(12), 1999.
3) Александр Шашин «Прозрачные параллели : Карпов и Капабланка». «Шахматный Петербург», специальный выпуск, сентябрь 2001.
4) А.Карпов «Сто победных партий». Москва, «Физкультура и спорт», 1984.
