- шахматная игра связана с перебором громадного (10 в 120 степени)  количества вариантов, поэтому доказать несостоятельность большинства шахматных рекомендаций  автора  практически невозможно; 

- многие рассуждения автора будут подкреплены  результатами исследований, проводимых сотрудниками ЗАО «Интеллектуальные игры»;

- читателям будет предоставлена  возможность самим проводить эксперименты, с целью выявления новых непознанных шахматных истин, при помощи соответствующего программного обеспечения, которое в недалеком будущем можно будет загрузить с сайта e3e5.com.

 В первой  лекции под названием - «Дерево», читатель получит минимум знаний, о так называемом «шахматном дереве перебора», тех знаний, которые будут необходимы для восприятия последующего материала. Во второй лекции - «Логика электронных монстров» будут описаны основные идеи шахматного программирования, показаны «хронические» недостатки современных шахматных программ. Начиная с третьей лекции – под условным названием «Логика случайного», а также во всех последующих лекциях, собственно и излагаются новые идеи, применимые для оценки шахматной позиции, разрабатываемые научным коллективом  ЗАО «Интеллектуальные игры».

Лекция  №1.  Дерево

 Диаграмма 1.

           В соответствии с шахматными правилами белые имеют возможность начать партию ходами коней или пешек. Например, пешка «а» может сделать ход а2 – а3.  Возможен также ход а2 – а4.  Легко  посчитать – восемь пешек  по два хода:  8 х 2 = 16  ходов. Кроме этих шестнадцати ходов пешками, возможны также ходы конями.  Каждый из двух белых коней  имеет по два  хода.  Конь b1 может прыгнуть на  a3 и на  c3.    Конь g1 на  f3 и на  h3. Всего четыре хода.

 Подведем  итоги. В начальной  позиции белые имеют возможность  сделать один  из  16 + 4 = 20   ходов.

 Нарисуем  дерево.  В основании дерева поместим исходную позицию.  Вверх  прочертим ветви. 20 ветвей по числу возможных ходов белых.  На  каждой  ветке  поместим  по одному листу.  Всего 20 листов. Каждый лист дерева представляет собой  позицию после одного из возможных  ходов белых.    

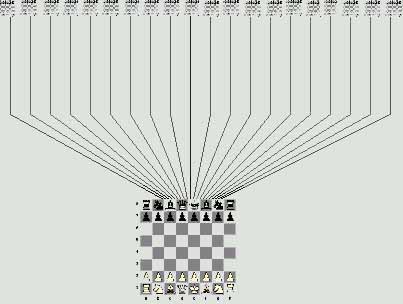
Рисунок 1.

 В свою очередь для любого первоначального хода белых существует двадцать возможных ответов черных: 16  пешками  и  4 конями.

            Продолжим рисовать дерево. От каждой из 20 позиций после первого хода белых вверх отрастают по 20 новых ветвей. На всех этих ветвях уже располагаются  20 х 20 = 400  позиций после первого хода  черных. 

 Читатель может сказать, что это дерево больше похоже на куст, поскольку совершенно не прослеживается  ствол – основное отличие дерева от куста. Но все же не будем нарушать не нами принятую терминологию. Мало того, мы и далее пойдем на поводу у математиков и программистов, которые не только называют этот куст деревом, но и очень часто переворачивают его с ног на голову. Для удобства дальнейшего путешествия по дереву присвоим каждому уровню дерева свой номер. Начальная позиция  будет считаться нулевым уровнем, все позиции после первого хода белых  будут располагаться на уровне под номером один, все позиции после первого хода черных  располагаются на уровне номер два, позиции после второго хода белых разместим на уровне номер три и так далее.

 Здесь следует заметить, что в дальнейшем при построении дерева мы будем строго следовать всем шахматным правилам за исключением чисто спортивных «человеческих» правил - правила «троекратного повторения позиции» и правила «пятидесяти ходов», благодаря которым в практической игре фиксируется ничья.  Обращаем также внимание читателя на часто применяемый в шахматном программировании термин – «полуход». Под полуходом понимают один ход белых или один ход черных, в нашем случае полуход соответствует переходу на один уровень дерева вниз. В то время, как «полный ход»  или просто ход, подразумевает два хода -  ход белых и ответ черных, что соответствует переходу на два уровня дерева вниз.

 Продолжим выращивание дерева, опуская  ветви из начальной позиции вниз, так что под нулевым уровнем окажется первый, под первым - второй, под вторым  - тре... Вот здесь нас и поджидает первая неприятность.

Неприятность  № 1.

 До второго уровня  дерево строится замечательно. На нулевом уровне мы имеем одну позицию. На первом уровне – 1 х 20 = 20 позиций. На втором  уровне – 20 х 20 = 400.  А сколько же позиций мы должны построить на третьем уровне?  Наивный читатель скажет – все очень просто 400 х 20 = 8000, и ... окажется не прав.  Для разъяснений вернемся на уровень № 2. А почему, собственно, мы так уверены, что на нем располагается 400 шахматных позиций? Ведь утверждение (на самом деле справедливое), что после любого первого хода белых, черные имеют 20 вариантов ответов, мы приняли без всякой  проверки. Чтобы строго доказать такое утверждение мы должны последовательно лист за листом нарисовать все 400 позиций - и никак иначе! А на третьем уровне мы должны будем нарисовать не 8000 позиций, а  - 8902 ! Дело в том, что количество возможных ходов белых в каждой из 400 позиций второго уровня различно. Так в трех наугад взятых позициях из второго уровня мы имеем  соответственно для белых -  32,  28  и  19  возможных  ходов.

Диаграмма 2.Возможных ходов белых - 32

Диаграмма 3.Возможных ходов белых - 28

Диаграмма 4.Возможных ходов белых - 19

 Простым умножением здесь не обойдешься : человеку чтобы точно подсчитать количество позиций на третьем  уровне придется израсходовать несколько десятков часов на последовательный перебор всех возможных  позиций. Именно поэтому «дерево» часто называют «деревом перебора». (Видимо, наиболее точным следует назвать его «деревом позиций»).

 Беда  заключается в том, что, начиная с третьего уровня, мы не можем по какой-либо простой формуле рассчитать количество позиций в дереве. Для точного вычисления количества позиций, на любом уровне дерева, нам необходимо все эти позиции получить путем полного перебора возможных вариантов ходов белых и черных фигур, начиная такой перебор из начальной позиции (с нулевого уровня). Иначе говоря, нам необходимо последовательно, уровень за уровнем, нарисовать (или построить) все  дерево, включая все его ветви и все его листы. Такая процедура человеку явно не под силу. Недалеко от человека ушел и современный компьютер. С помощью обычного персонального компьютера за 7 часов удается  построить дерево, включающее максимум  - 7  уровней.  При этом на третьем уровне количество листов дерева 8902, на четвертом – 197281,  на пятом – 4865351. Следует также обратить внимание на то, что трехуровневое дерево компьютер строит за –2 сек, пятиуровневое -  за 2 мин., а шестиуровневое – за 1 час.

 Неприятность №2

Неожиданно выясняется, что наш стройный подход к выращиванию дерева на листе бумаги (или с помощью компьютера в его компьютерной памяти) оказывается   практически бессмысленным. Дерево слишком быстро растет! Никакой компьютер никогда не построит дерево соответствующее,  например,  50 ходу черных  - стоуровневое! дерево. На это просто не хватит вычислительных мощностей (компьютерной памяти и быстродействия). Проиллюстрируем это, приведя примерное время вычисления количества позиций дерева для уровней, начиная с шестого, на компьютере типа «Pentium-III».

6         ~  1 час

7         ~  сутки

8         ~  далее объем работ возрастает настолько, что на их выполнение потребуются недели непрерывных расчетов компьютера.                                                              

       В действительности мы понимаем, что дерево существует независимо от нашей неспособности его построить. Человек, в отличие от компьютера, может мысленно продолжать строительство дерева, продолжая его вниз и вширь, насколько хватит фантазии.     

 В дальнейшем число возможных ходов белых или черных в какой-либо позиции будем называть «подвижностью». Понятно, что в позициях, где ход белых (четные уровни дерева), речь может идти только о подвижности белых фигур. Соответственно в позициях, где ход черных (нечетные уровни), можно говорить о подвижности черных фигур.  Наверное, этот термин не очень удачен для такого понятия как шахматное дерево, но в последующих рассуждениях, когда начнется собственно игра в шахматы, этот термин  нам очень пригодится. Ясно, что подвижность в любой позиции - это есть количество ветвей в дереве,  которое произрастает из этой позиции (листа).

Дерево позиций – дерево перебора.

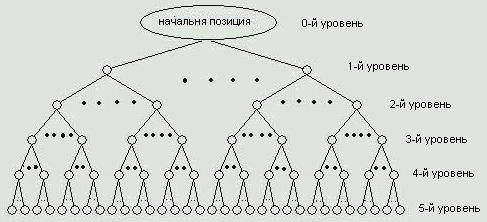
Рисунок 2.Из начальной позиции дерево растет вниз до бесконечности

Несмотря на то, что мы не можем точно описать дерево до уровня, который включает большинство человеческих партий (160 уровень – 80 ходов),  в виду его колоссальных размеров, все же, пользуясь простыми  логическими методами, мы можем установить некоторые присущие дереву свойства:

Свойство № 1  -  в дереве встречаются  одинаковые позиции. Действительно, уже на третьем уровне среди 8902 позиций встречаются несколько начальных позиций. (Одна из начальных позиций может возникнуть на третьем уровне дерева после следующих ходов 1. ¤f3   ¤f6. 2. ¤g1   ¤g8).  Аналогично рассуждая, легко прийти к выводу, что в дереве встречаются и различные множества одинаковых «неначальных» позиций.

Свойство № 2 – дерево бесконечно – это прямо вытекает из  Свойства №1  и  принятого нами условия, что мы игнорируем  шахматные правила «троекратного повторения позиции» и «пятидесяти ходов».  Действительно, из любой  начальной позиции третьего уровня можно построить точно такое же дерево, как из начальной позиции первого уровня. Таким образом,  на уровнях 0, 3, 7, 11, 15 и далее до бесконечности встречаются начальные позиции.  

Свойство № 3 – В дереве существуют тупиковые ветви. Действительно, из тех позиций дерева, где зафиксирован мат или пат, ветви не растут. (Пользуясь принятой терминологией, можно сказать, что подвижность в таких позициях равна нулю).

 Конечно, свойства дерева не исчерпываются перечисленными выше тремя пунктами, но именно к этим трем мы постоянно будем возвращаться  в последующих лекциях.

В завершение первой лекции, следует обратить особое внимание читателей на то, что дерево содержит все партии, которые когда–либо были сыграны людьми, а также все партии, которые ими еще будут сыграны (дерево включает все существующие электронные базы шахматных партий). Дерево содержит всю шахматную информацию, которая интересует шахматистов. В дереве,  зашифрованы ответы  на все вопросы, связанные с оценками той или иной позиции. Дерево несет в себе и ответ на вечный вопрос - «Белые начинают и ... ?».