17.01.2005
V.B.Nevzorov. Past, present and future of chess rating
V.B.Nevzorov. Past, present and future of chess rating
1. Introduction
Today rating is an indispensable attribute of any chess player of sufficiently high class. People greet them and take leave of them according to their rating. High rating qualifies to take part in tournaments of the highest category (and the categories of tournaments themselves are determined according to the average rating of the participants), and hence the possibility to pretend to high fees. Reaching of a certain level of rating is a necessary condition for getting a title of master or a grand master. Rating of a participant (or an average rating of a team) is taken into account at drawing of lots in competitions that are carried out according to the Swiss system. The higher rating of opponents provides the higher place in case of equality of points scored in a tournament. Young chess players are striving to get their start rating as soon as possible, and top chess players, minimize the number of competitions or choose them carefully in order not to run the risk of losing theirhonorary place. Belated transfer of money for calculation of rating by the Federation may become a tragedy for chess players of the whole country, having deprived them of the right to take part in professional tournaments. Perhaps, only professional tennis players are as solicitous and jealous about their rating as the worshippers of Kaissa. So, rating is a phenomenon (with its merits, drawbacks and problems), without which it's impossible to imagine the chess world at the beginning of the XXI century. However less than 40 years ago chess players, meeting each other, didn't ask “What is your Elo?”, didn't wait for the next rating list of FIDE to find out their new coefficient, to learn about changes in top ten or hundred of the best (according to the calculations of the authors of that list) of his colleagues. Certainly, there were various ways of ranging in many kinds of sport before: the best sportsmen of the year, of ten years in the country or in the world were determined. In most cases ranks were given to sportsmen according to their results and taken places. There were even attempts to compare sportsmen of different kinds of sport (first of all of track and field athletics), compiling special tables of converting, for example, fraction of seconds in woman's hundred meters race into centimeters of shot-putters among men. In chess there also was its own hierarchy: a world champion, challengers for that title, top-level (but not challenging for the champion's title) grand masters, international masters, national masters, etc. Every three years the chess world was watching the attempts (successful or unsuccessful) of a second-best chess player, who was called "a challenger for the chess crown", to change places with a world champion – number one in FIDE classification. “Challenger” is a title, won after selection, in which any chess player, sifted out in country's championships, zonal and interzonal tournaments and challenger's matches, could formally take part, but practically only a narrow circle of the strongest grand masters could contend for it. As for the subsequent (third, forth, …) numbers in the chess world, they were not assigned to anybody officially or unofficially. Except that the loser of the final of Challenger's circle might have been called the third one and he could have enjoyed privileges in the next circle. Chess elite could also "sort out" their personal relationship in international tournaments, but it was almost impossible to compare levels of average masters from such advanced chess countries as the USSR and the USA (except that according to the following principle: "master X in the championship of the USA was defeated by GM Benko, and master Y in the semifinal of the championship of the USSR had a draw with GM Z, who in his turn in the final had a draw with Mikhail Tal, and the latter in the Challenger's tournament in 1959 against Benko had won 3,5 points from 4, therefore Y must be placed higher”). Even if the opponents (say, A, B and C) had an opportunity to meet each other frequently, it was difficult to arrange them according their strength, if for example A constantly defeated B, but always had trouble in the games against С, who in his turn had no luck against В (there are a lot of such examples in chess history). Despite that, a questions like "Who was the strongest in his best years – Alexander Alekhine, Mikhail Botvinnik or Robert Fischer?" were asked fairly often and there were even attempts to use various statistical materials to answer such questions. Such attempts to compare sportsmen of different epochs and continents led in XX century to the appearance of the first rating systems, which were used in some countries, and in 1970 one of them, the system of individual coefficients of Arpad Elo was officially accepted by FIDE for comparison of the results of chess players.
For the past thirty odd years the Elo system covered tens of thousands of chess players of different qualifications, most of whom didn’t have and don’t have now any practical chance to play with each other, but, having been united by one rating list they can exclaim “Gensunasumus!”. Perhaps this system was so widespread at the end of the last century due to the fact, that the authority of the world championship matches (and consequently of the latter-day world champions) was no more incontestable after undefeated Robert Fischer gave up chess, politically loaded duels between Victor Korchnoi and Anatoly Karpov, appearance of competitive chess federations and associations with their own champions, who refused to play with each other, and a quick putting of chess on a commercial footing. All that led to necessity to have means of numerical estimation of results and potentials of chess players. There was required a system that was able to determine, who of the great number of acting (according to different versions) world champions is truly the strongest one. Sponsors of the numerous commercial championships also wanted to invite truly the strongest (according to some acknowledged standards) players to those tournaments. The system of coefficients of Arpad Elo became the official system of FIDE. However in the number of federations there were accepted a bit different estimations of the results of the chess players, who were the members of those federations. Those systems (for example, rating of USCF) are more or less correlated with the Elo-rating. A professional rating (slightly different from the Elo-rating), which was developed by Ken Thompson is also popular among top chess players. There is also a number of other systems (for example, Glicko and Glicko-2, suggested by professor M.E.Glickman), the authors of which try to improve the official rating system of FIDE. We'll analyze different advantages and disadvantages of Elo-system and try to outline ways of its improvement. We want to note that there is a number of views on problems of ranging of strength of chess players, some of which are supported by us and with some we fundamentally disagree. Below we'll try to back up our discourse with probability-theoretical and statistical arguments.
2. Main requirements to ratings
Any ratings system is an attempt of ranging actual chess players, based on their results. Certainly, it'd be interesting to get not only the places, occupied by certain chess players in a long list of participants of numerous competitions, but also to try to represent numerically the chess strength of the players, being compared, at some scale. Moreover, the system must be dynamic enough to represent quickly the changes that take place in the chess world. At the same time the system must contain elements of stability such as some absolute (fixed or invariable during a long period of time) levels, which serve as orienting points for categorizing of chess players. At the same time while it's important for the best 50-100 chess players how their ratings correlate numerically, it's of interest for the majority of chess players into which cluster falls their rating and what is the recent dynamics of it. It's not so important, for example, who ranks a place in a list before you under No. 5345 (it’s possible to determine with a great difficulty, having worked up a large alphabetical data list), and it is more important, how close you are to the mark 2400 or to what extent your chess strength has increased for the last three months. For organizers of competitions it's important that most of participants have official ratings and it's desirable not to have equal ratings among them. The probability of appearanceof chess players with equal ratings increases while the number of chess players increases. That's why if, for example, in the first Elo-rating lists values were rounded to numbers, divisible by 5, then now FIDE uses rounding to 1 point at the end, but that also doesn't save from the appearance of equal ratings. For example, even in relatively rarefied top of the last FIDE rating list two players among first 50 have rating 2687, other two players – 2682, another two players tie 26th – 27th places with the result of 2676, there are three chess players both on levels 2669 and 2663, two GMs have result 2660. Perhaps in the future we'll have to calculate ratings, rounding values off to one or two decimal places to "distinguish" players from each other. It's important not to increase calculation accuracy, but to avoid some uncertainty at categorizing participants of competitions, and also to use rating factor in case of equality of other characteristics more effectively. Authors of some systems pretend to "count back", using the database, and to compare ratings of the acting chess players with those who have already quitted the scene. This approach seems to be rather non-natural. Thus they try to answer the question like "who will win in the struggle between a whale and an elephant?". The point is that although in the chains of games A against B, Вagainst С, Сagainst D,..., X against Y, Y against Z, which are used to get from a chess player A of the beginning of XXI century to a chess player Z, who played at the end of XIX century, appear the same names (Вand В, Сand С,...), but, in essence, these are the chess players of different strength. And in the issue of such calculations the measure of inaccuracy accumulates very much. Moreover even the same chess player with rating for example 2700, could be an undisputed leader of the chess world in 1980 and with the same rating can even be outside the top ten of chess players 20 years later. This effect can be explained as follows. Imagine that n points are thrown at some interval. With an increase of n these points fill the interval more and more densely and the extreme (both on the right and on the left) points approach close and closer to the ends of the chosen interval, though arithmetical average value of all the coordinates can be constant. According to what has been said, a maximum, one or two decimal place value of a chess player's rating must increase along with an increase of a number of chess players, who received ratings. That's why the systems, where it's suggested to contend with "inflation" of the highest ratings, moving the scale so that, say, a rating of the tenth chess player would be a constant, for example, 2700, seem to be not very felicitous. More natural would be to admit the presence of "inflation", observing the dynamics of so-called "one-percent points",i.e. ratings of the fiftieth number in a rating list, consisting of 5000 chess players with ratings, of the seventieth number, when this list has increased up to 7000 players, of the one hundred twentieth number with 12000-players list etc. These points must keep steadiness, not changing noticeably in the course of time. The situation with "two-percent", "three-percent" and so on points is analogous. This can be explained by the fact that even in case of absence of "inflation" the situation, when the number of chess players with the rating, say, 2400, increases proportionally to the number of chess players included in the rating list, is quite natural. That's why an increasing of a number of chess players who have official titles in FIDE if receiving of these titles is concerned with reaching of certain levels of rating mustn't be surprising.
The given arguments show that it's certainly possible to calculate rating of Morfy, Steiniz, Capablanca, but it makes sense to compare these ratings only with the ratings of theircontemporaries, calculated in the same way.
Let's consider one more circumstance that plays an important role in calculating of ratings. Imagine that all the chess players are divided into some non-overlapping groups and compete only inside their groups. Calculation of their ratings will give an idea of relations inside the groups, but won't permit to compare participants from different groups. Carrying the situation to an absurdity, we can consider two chess players, who play only with each other. If one of them wins constantly, he'll be able to increase his rating without limit and eventually to exceed even a record for today rating of Garry Kasparov, but it doesn't mean that this player will be called the strongest in the world. However you may object that the opponent, who loses all his games, will as well decrease his rating vastly to the lowest possible level, will leave the rating list and cease to provide his more successful opponent with rating points. But there are systems (for example, the system of USCF), in which it's impossible to decrease one's rating below a certain level. That's whyin any case, if a system pretends to a commonality, it must provide for "mixing" of the participants for comparatively visible period of time. By "mixing" we just mean the situation, when long-term groups of constant chess players, who don't play with other players of the list, aren't formed.
Authors of different systems consider as one of the main advantages the possibility to predict results of chess players according to their ratings. It seems to bedisputable that probability of exact prediction can be close to one. Say, if we are guided only by the last published rating, then expected with the highest probability data of the next rating list must fully coincide with the previous ones. But such coincidences have never been met yet, and they are possible, perhaps, only if for three months between successive publications of two ratings not a single chess game is played. Moreover, it's possible to predict the next rating exacter, if a long-term behaviour of it is well known, which permits to get extra useful information about rating as some random process. But also in this case there must be similar information about all the opponents of a chess player, whose future rating we're trying to predict. It's possible to try to predict results of a certain chess player during a period of time. It's difficult to do that, if the matter concerns one game. Let us suppose, for example, that the comparison of two rating lists led to prediction that A must score 75 percents in the game against B, i.е. the most probable result must be 0,75 point. It's clear that any true result (0, ½ or 1) will differ from prediction not less than in one third. Certainly, an error of rounding will be less in case of predicting a summary total of a great number of games. It's possible to produce more reasons explaining why the exactness of prediction can't be very high. Any value of rating is a kind of averaging of chess player's strength level. This level can change for various reasons even during one comparatively long tournament. But situations, when a chess player doesn't play for a long time and his rating remains constant during this time are frequent. Therefore only with great reserve it's possible to consider that official rating of a chess player answers his today's level of playing. For a long period of time FIDE rating was calculated with rounding to numbers divisible by 5, that's why most of the games in chess databases contain data about ratings of chess players with such a precision. Note that the given rounding also gives some measure of inaccuracy, because an expected value of scored points with an increase of rating at 5 points changes already at one percent. Essentially larger measure of inaccuracy is brought by the system of calculation, in which the colour of pieces of opponents is not taken into consideration. We'll speak about that in greater detail below, and by now we’ll note that the right to start is estimated approximately at 40 ratings Elo-points (in case of equality of ratings a chess player who plays with white pieces must score on the average not 50, but about 55 percents of points). Rating can change considerably depending on the period of time, during which games for the next rating calculation are collected (a year, half a year, current three months, taken for calculation of FIDE rating, a month). The influence of this factor is especially noticeable when a chess player during this period has a high number of successes (or failures), for example, such as accompanied Robert Fischer in his Challenge's matches before his winning of the champion's title. If his rating was re-calculated already after the first match, won with the score 6:0, then the result 6:0 of the next match would be more expected and would provide Fischer with a considerably less increase of rating. That's why if there are technical possibilities, rating should be re-calculated after each game (it's ideally) or at least once a week. Certainly, it is not necessary that the re-calculation "after each game" is made on that day when a game is played, but immediately after a tournament is finished. All these arguments show that it makes no sense to strive for a high degree of accuracy of prediction of future results basing on the existing rating. Statistical conclusions, made by authors of some new rating-systems and by critics of the old ones, show that the best systems from the point of view of prediction provide an accuracy of prediction of future results about 85 percents. Inclusion in the calculation of the games with different time-limits is one of the problems under discussion. Many authors suggest to consider all the games, played by a given chess player for a reporting period, but to include them in rating with different coefficients. Say, if classical games are taken with the coefficient 1, then "30-minutes" games, as for example suggested by Jeff Sonas, must be considered with the coefficient 0,29, and "five-minutes" games, in his opinion must make their contribution to the rating of a chess player with a value 0,18. The necessity to consider all the games is motivated by the fact that each of them provides certain information about the strength of a chess player, and this information must influence rating. It seems that the roles of classical games and blitz ones in the history of chess differ essentially. Hardly anybody can remember now at least one fragment from the blitz games, played by Mikhail Tal, who brilliantly played both classical and blitz games, but there is a quantity of works, which deal with his "classical" creative heritage, though, in opinion of Jeff Sonas, 6 games, played by opponents for an hour, are equivalent to one game, played with classical time-limit. There may be an answer that in tennis ratings matches, played on grass and ground tennis-courts, are estimated equally, and in track and field athletics a specially selected system of points permits to ascertain a winner in decathlon, where sportsmen compete in the kinds of sport, which are separated more widely than "classical" and "rapid" chess. As for tennis, there is a proven system of tournaments, which are practically obligatory for all the players from the top of the rating list. All the tennis-players are placed on an equal footing, they participate in approximately equal number of competitions, which are carried out at tennis-courts of different kinds. Multiathlon is a special kind of track and field athletics, in which, as a rule, sportsmen who show high, but not outstanding results in single kinds of this multiathlon achieve success. A kind of analogue of chess all-round could be also arranged, which will combine in one tournament, for example, classical and blitz chess with bridge and billiards, but this would be another kind of all sports. Nevertheless, taking into consideration that percentage of chess games with classical time-limit decreases every year, and in the matches, which are carried out according to classical rules, for determining a winner in case of a draw regulations suggest to play "rapid" games, a flexible system of calculation of rating should be thought of, according to which not only the games with classical time-limit, but also all the games with some reasonable (for example, not less thanan hourand a half) time-limit will be considered.
3. Mathematical models of chess ratings systems
Above it was already mentioned, that there are different variants of ranging chess players according to their level. The most commonly used is the accepted by FIDE system of Arpada Elo. A number of other systems are various modifications of Elo rating. Let’s consider some mathematical basis of construction of such systems.
One of the first systems of chess players ranging was offered 50 years ago. It was called Ingo-system in honor of a Bavarian town of Ingolstadt, which is a native town of the author of this system, Anton Hoesslinger. The essence of this system was in the following. The rating of the chess player was recalculated or determined for the first time on the basis of the games played by him for a certain competitive period. The average rating Rср of his opponents in these games and the percentage Π (0 ≤ П ≤ 100) of scored in these games points. Then the new rating R was calculated by the formula
R=Rср +(50-Π). (1)
Let's note that this system assigned the lower rating to the stronger player. The previous rating of the player was not taken into account in his new rating, but was taken into account for the calculation of Rсрfor his opponents. Formula (1) was a simple one, but a considerable dependence of the rating on the result of several last games was its serious drawback. The important fact applied later in the majority of other systems was the dependence of the new rating on the average rating of the opponents and the differences between the achieved result and an expected result of the chess player (in Ingo-system the 50-percent result was considered to be the expected one).
The following important step to the creation of current official FIDE system had been made by Arpad Elo. He took into consideration, that the strength of the chess player even during one competition is not a constant value; it depends on many random factors. For each player Elo suggested to pair a random variable ξ, having a normal (or as it is called in the theory of probability, Gaussian) N(R, σ) distribution with expectation R and with rootmeansquaredeviation σ = 200 where R is a rating of the given player. The great value of rootmeansquaredeviation which is equal to the variance σ2= 40000, has been chosen from a reason of convenience of arranging of big number of players on a numerical scale.
Let's take two chess players whose level of game is described by random variables ξ1 ~ N(R1 ,σ) and ξ2 ~ N(R2, σ), where R1 and R2 are their ratings. Elo assumed that in such situation the first of these chess players in a game against the second player should score a part of points which is equal to the probability of event { ξ1> ξ2}={ ξ1- ξ2>0}. A part of points of the second player scored in a game against the first one, will be equal to the probability of event { ξ2> ξ1}={ ξ1- ξ2<0}. We shall note that, probably, this idea works better in the games where only one of two results, either a victory or a defeat is possible, but Elo extrapolated this principle to chess where, as it is known, most of the games are drawn. It’s possible to find necessary probabilities at various values of ratings difference Δ=R1-R2 using the tables of values of function of normal distribution law.
Indeed, if to assume, that ξ1 and ξ2 are independent random variables having normal N(R1, σ) and N(R2, σ) distributions, then, as it is known, the difference of these variables η= ξ1 - ξ2 is also normal with mathematical expectation Δ=R1-R2 and variance 2σ2, i.e. rootmeansquare deviation
σ0= σ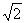 =200
=200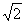 ≈282,8. Let us denote the standard normal random variable with a zero mathematical expectation and a unit expectation, the one, tables correspond with, by ν. It is possible to make use of the fact that
≈282,8. Let us denote the standard normal random variable with a zero mathematical expectation and a unit expectation, the one, tables correspond with, by ν. It is possible to make use of the fact that
η has the same distribution, as the variable σ0ν+ Δ has. Then
P{ ξ1> ξ2}=P{ ξ1- ξ2>0}=P{ σ0 ν+ Δ>0}=
P{ ν>- Δ/ σ0}=P{ ν< Δ/ σ0}=Φ(Δ/ σ0), (2)
Where Φ(x) is the function of distribution of the standard normal law, the tables of which are often used. Using these tables, at various Δ it is easy to find wanted probabilities. For example, if Δ =20, then Δ=20, тоΔ/ σ0=1/10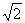 ≈0,07 and
≈0,07 and
P{ ξ1> ξ2}≈ Φ(0,07) ≈0,53.
According to Elo this means that the first player with a rating by 20 items greater should score 53 percent of possible points in the games against the second player, leaving 47 percent for the second one. Such values have been found for a wide spectrum of values Δ. At the same time Elo prepared a kind of reversed tables. Here is an example. Let us assume that we are interested in such a difference of ratings Δ that the first chess player should score 84 percent of points in the game against the second player. It means, that such value Δ that the right member (2) is 0,84, is to be found. Using the same tables of normal distribution we find, that
Φ(x*)=0,84,
If x*≈1, then we find Δ from the formula
Δ/ σ0=1
And Δ≈ 283 is obtained. Thus a chess player should have a rating of about 280 items greater to score 84 percent of points in the games against his opponent. Thus, in the new tables each value p=0,50 (0,01) 0,99 is assigned to the difference of opponents’ rating which should provide the first one with a part of points p in the games against the second one. If p <0,50 it is sufficient to reverse the chess players and then to find the value of Δ, corresponding 1-p.
Having prepared these two tables, Elo suggested the following system of rating recalculation in relation to the results of the games played for a certain period of time (a year, half a year, three months). We count an average rating of all the opponents Rср and a difference Δ=R- Rср between the given player and his averaged opponent. Using the first table we find an expected part of points p which the player should have scored in the game against the averaged opponent. Then, this part of points is compared to the part of really scored points pN (it is possible to find the difference between the expected and scored points, instead of comparing parts of scores, one difference is easily deducted from the second one if we know the number of the played games). We shall remind, that in Ingo-system the expected part was 0,50. Certainly, we could (almost as in Ingo-system) simply take percentage pN as a source material, using it we could find in the second table such value ΔN that would provide such result, and could take RN=Rср+ ΔN as a new rating. Such approach would not be flexible enough and would sharply change sequential ratings from one recalculation to another. Elo has suggested taking with some weight coefficients both old R and a new RN, a value of ratings, and it is possible to do this even not calculating RN, but using the difference of scored and expected points or the parts of scored and expected points. For this purpose it’s possible to use the following formula
RNew=R+K(pN-p), (3)
Where RNew and R are accordingly the new and the old ratings, pN and p are the scores and expected percentage of points, and K is a coefficient, the choice of which can depend on the number of games played for the period under review, on the number of games, the old rating was based on, on the level of the old rating (for example if R>2400 there is one value of K, and another one, if R<2400, etc.). The choice of the coefficient affords to make the rating more or less dynamical. We shall remind, that in formula (3) it is possible to replace the difference
pN-p by the corresponding difference of the scored and forecasted points. Coefficient K can depend on the number or on the part of the games played for a certain period of time, helping the last games to contribute more or less significantly to the rating.
This is an approximate structure of many rating systems. Some of them have their own specific features. For example, in the Professional rating or in Glisco-system the scatter of rating values (which is a rootmeansquare deviation in Elo system) is not constant, and it varies with time. In the USCF system (of the American chess federation) the rating of a chess player can not be lower than thresholds values. So, if someone has reached once a rating of 2450, his rating can not be less than 2200. Advantages and disadvantages of Elo-type ratings have been mentioned above. One of the problems is that Elo system does not take into account the colour of pieces of a chess player which affects the result of the game significantly, giving White an advantage of 40-50 rating points even when the ratings of the opponents are equal.As it was mentioned before, this system ignores to some extent an opportunity of drawn games. These considerations can be essential in the situations when even small distortions of rating can affect the ranging of the opponents. It concerns, first of all, 50-100 best chess players of the world. We suggest little changes that, in our opinion, would help to reduce the mentioned drawbacks.
Let's have a look at some statistical data showing the advantage of white colour. The data were prepared by Vladimir Balakirev on the basis of games results for the period of 1998 - 2004 taken from MegaDatabase. The following values were analyzed
T(Rw,Rb)=(Nw-Nb)/N, where Nw is the number of the games won by White, Nb is the number won by Black and N is the total number of games with a fixed difference of chess players’ ratings, who had white (Rw) and black (Rb). Rw and Rb were fixed in sequence at levels of 2300, 2310, 2320, …, 2600, such games were chosen from the database that those who had white had rating Rw, and Black had the rating Rb. Values T(Rw, Rb) were calculated on the basis of all these games. It was necessary to trace, at which difference of ratings value T(Rw, Rb) (which is equal to the difference of parts of points scored by White and Black accordingly in all games played by the opponents who have these ratings) becomes negative. For example, values
T(2300,2300 =0,029; T(2300,2310 =0,003; T(2300,2320 =0,014;
T(2300,2330 =0,015; T(2300,2340 =0,009; T(2300,2350) =-0,023;
T(2300,2360) =-0,002; T(2300,2370) =-0,0041
show, that 40 rating points advantage of Black does not provide him the
advantage over White, but at 50 points difference this advantage is quite tangible.
At 2400 rating of White such phenomenon occurs between 30- and 40-points difference:
T(2400,2430 =0,001, and T(2400,2440) =-0,011. Then, T(2500,2530 =0,002, and T(2300,2340) =-0,012, etc. For all Rw values it was noticeable that the transition from the advantage of White to that of Black occurs in the interval 30 up to 50 points ratings difference. To demonstrate this clearly, all the games with a fixed differences of ratings Δ=0,10, 20 were grouped together, … (they were not subdivided according to the rating of White) and similar values T(Rw,Rb) were calculated (we shall call them T(Δ)). We obtained T(0 =0,033, T(10 =0,014, T(20 =0,018, T(30 =0,006, T(40) =-0,08, T(50) =-0,015, T(60) =-0,018, T(70) =-0,031, i.e. here statistics shows again, that critical value of ratings difference is about 40. Unfortunately it’s impossible to draw more exact statistical conclusions as in the majority of the games that were used for calculations, the rating was accurate to 5 points (for a long time Elo rating had been rounded off to such accuracy). Therefore we shall suppose Δ=40 to correspond approximately the advantage which is provided by white colour of pieces. We shall calculate this value Δ in another way, using a bit different statistical conclusions.
It was also told above that Elo suggested to represent a level of a chess player in a certain game (or even during some period of time) as a normally distributed random variable, mathematical expectation of which is described by the rating of a chess player. To some extent such a representation can be used because a chess game is formed from a rather large number of random interactions, each of which can bring some micro-advantage to one or another chess player. It's known from the theory of probability (this fact is called central limit theorem) that sums of a large number of random summands approach very well to random variables, which have normal approximation. Every chess player can play better or worse than his average level in a given game. And even a player whose rating (average value) is lower than that of his opponent, has a chance to show a higher level of playing than that of his opponent.
Turning back to the idea of Elo, let's suggest that the level of playing of opponents can be described by random values ξ1 ~ N(R1 ,σ) and ξ2 ~ N(R2, σ), where R1 and R2 are their ratings. Parameter σhas a scale character (in which units should the result be measured – in meters, in yards or in centimeters?), it's not very important for ranging of chess players and is needed only for reasons of convenience (as we remember, Elo has σ=200). In Elo-system the expected part of points, which a first player will get in the game against the second one, was determined simply, as a probability of the fact that ξ1> ξ2, i.е. the first of the players will play, though not considerably, but better than his opponent. Actually, sometimes, even a great, at first sight, advantage, achieved in a game by one of the opponents, isn't sufficient for a win. It means that for a win a player needs not only to surpass an opponent, but to surpass him considerably. That's why let's assume that for a win of the first player it's necessary that not the event {ξ1- ξ2>0}, but the event {ξ1- ξ2>δ} takes place, where δdenotes the level of accumulated advantage, which is sufficient for a win. With the help of statistical procedures we can find the value of δ. Let's introduce one more unknown Δ, which will denote such advantage of Black in rating which can neutralize the right of the first move of his opponent. Let ξ1 denote the strength of White who has rating R1, and ξ2 – the level of Black with his rating R2. Taking into account the colours, the real difference of ratings is R1-R2+ Δand, comparing with formula (2), the formula of White's win probability can be derived:
P{ ξ1- ξ2+ Δ > δ }=P{ σ0ν+ R1-R2+ Δ> δ }=
P{ ν> (δ - Δ –( R1-R2))/ σ0}=P{ ν<( R1-R2 -δ + Δ ) / σ0}=
Φ(( R1-R2 -δ + Δ ) / σ0), (4)
where
σ0=200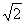 ≈282,8.
≈282,8.
We can similarly get that Black's win probability looks as follows
P{ ξ1- ξ2+ Δ <- δ }= Φ(( R2-R1 -δ - Δ ) / σ0), (5)
and the probability of a draw can be found by formula
P{ - δ <ξ1- ξ2+ Δ < δ }=
1- Φ(( R1-R2 -δ + Δ ) / σ0)- Φ(( R2-R1 -δ - Δ ) / σ0)=
Φ(( R1-R2 +δ +Δ ) / σ0) - Φ(( R1-R2 -δ + Δ ) / σ0). (6)
In formulas (4)-(6) two unknown values appear (we've forgotten for a while our previous conclusions, concerned with estimation of Δ) and they can be determined by statistical methods. For the sake of simplicity let's consider the case, when White and Black have an equal rating (R1=R2). MegaDatabase presented 8421 games (for the recent 6 years), in each of which the ratings of White and Black were equal (within the accuracy ofround-up). From these games 2461 (or 29,2%) were won by White, and 1696 (or 20,1%) – by Black. At the right-hand sides of (4) and (5) let's take R1=R2 and equate the received expressions to 0,292 and 0,201 correspondingly. We'll get the equations
Φ((Δ -δ ) / σ0)=0,292
and
Φ((-δ - Δ ) / σ0)=0,201.
By tables of normal distribution law function we can find that
(Δ -δ ) / σ0=-0,55
and
(-δ - Δ ) / σ0= -0,84.
Hence we can get that Δ≈41, and δ≈197. A rational round-up permits to believe that the advantage of the first move indeed can be estimated approximately in 40 rating points in Elo-system, and in order that one chess player defeated the other one, he must get in the game an advantage of approximately 200 points. For example, let's consider opponents one of whom is playing with White and has rating is 2560, and the other one with a rating 2600. Taking into consideration the color of pieces, we can consider that two equal opponents with rating 2600 are playing. To find a probability of win of the first player we need to calculate the probability for players with equal ratings
P{ ξ1- ξ2 > 200}.
It's equal to
1-Φ(200/ σ0)=1- Φ(0,707) ≈0,24.
Black has the same probability of the win, and a draw can be supposed with probability 0,52. Naturally in this case we'll expect that both of them will score 50% points each. In the Elo-system an expected result of a player with 40 points less rating than that of his opponent is 44 percents, and his opponent (although he is playing with Black) must score 56 percents. Thus the possibilities of Black are overestimated by more than 10 percents (instead of 50 he has a task to get 56 percents). So, taking the color into consideration, a win and a draw of Black will be estimated (from the point of view of rating increment) higher than the similar results of White.
Certainly, the values of Δ and δ were ensued from statistical processing of a great number of games, in which the rating of players lies in a wide range from 2300 till 2700. If to be limited to the more even composition of the participants of our statistical analysis, for example, to the players, whose rating lies in more narrow ranges 2300-2400 or 2700-2800, then the values of the parameters, in which we are interested, can vary though not verysubstantially from range to range. To some extent it's related to a supposition which is used in some rating systems that the variance (the degree of scattering) of the level of playing and results of the chess players decreases with increasing of rating of players. It can affect so that a root mean square deviation of above analyzed differences ξ1- ξ2 will be not σ0=200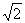 ≈ 283, but a smaller value. This hypothesis needs a further careful testing.
≈ 283, but a smaller value. This hypothesis needs a further careful testing.
Many of the chess players already agree that results that were achieved by White and Black pieces should be estimated separately when re-calculating the rating. We hope that suggested by us (the more correct one as it seems to us) system of calculation of expected results in case of playing with White or Black pieces won't require an essential reconstruction of the existing principles of chess players ranging.
