(lectures of the chess amateur)

The reader is given the opportunity to observe the game of chess from the most common positions. It may be the first time, when an attempt to prove the strategic purposes of game with the help of "not chess" methods is made. Some practical recommendations given in the lectures can seem to be strange and even harmful. The following can be told to justify my ideas:

- game of chess is connected with enumeration of the enormous (10 raised to the 120th power) number of variants, thus it is almost impossible to prove an unfoundedness of the majority of author's chess recommendations; 

- many reasonings of the author will be supported by the results of the researches carried out by employees of the Joint-Stock Company « Intellectual games »;

- readers will be given the opportunity to carry out experiments, in order to reveal new, unknown chess truths, by means of the appropriate software which can be loaded from a web site e3e5.com in the near future.

In the first lecture, which is called "The Tree", the reader will receive a minimum of knowledge about so-called «a chess searching-tree», which will be necessary for perception of the subsequent material. In the second lecture – “The logic of chess monsters” the basic ideas of chess programming will be described, "chronic" drawbacks of modern chess programs are shown. Starting from the third lecture - under the conventional name “The logic of the casual”, and also in all subsequent lectures, the new ideas that can be applied for an estimation of a chess position, developed by scientists of Joint-Stock Company «Intellectual games» will be stated.

Lecture № 1. The tree

Diagram 1.

According to chess rules White has an opportunity to start a game with moves of knights or pawns. For example, the pawn "a" can move а2 - а3. The move а2 - а4 is also possible. It is easy to count - eight pawns, each has two moves: 8 х 2 = 16 moves. Except for these sixteen moves of pawns, the knight's moves are also possible. Each of two white knights has two moves. The knight b1 can jump on a3 and on c3. The knight g1 can jump on f3 and on h3. Only four moves.

Let's sum up. In the initial position White has an opportunity to make one of 16 + 4 = 20 moves.

Let's draw a tree. In the basis of a tree we will place an initial position. Upwards we will draw branches. There are 20 branches according to the number of possible moves of White. On each branch we will place one leaf. The total of 20 leaves. Each leaf of the tree represents a position after one of the possible moves of White.

                     

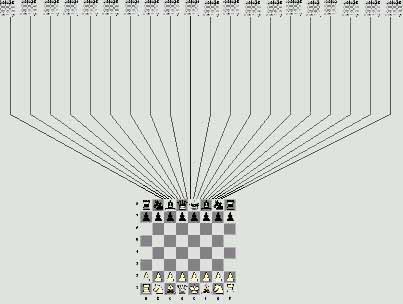
Picture 1.

In turn, for any initial move of White there exist twenty possible answers of Black: 16 moves of pawns and 4 moves of knights.

            Let's continue to draw our tree. 20 new branches grow upwards from each of 20 positions after the first move of White. On all these branches there are already 20 х 20 = 400 positions after the first move of Black.

The reader can argue, that this tree is more similar to a bush, because the stem - the main distinctive feature that differ a tree from a bush - is not traced at all. But nevertheless we will not violate the terminology that is accepted not by us. Besides, we will be led further by mathematicians and programmers, who not only call this bush a tree, but also turn it on its head very frequently. In order to make our travel along the tree more comfortable we will give the number to each level of the tree. The initial position will be considered as a zero level, all the positions after the first move of White will be placed at a level number one, all the positions after the first move of Black are placed at a level number two, the positions after the second move of White we will place at a level number three and so on.

It is necessary to notice, that further when constructing a tree, we will strictly conform to all chess rules with the exception of the purely sport "human" rules – the rule of " triple repetition of a position” and the rule of " fifty moves”, due to which draw is stated in practical game. We also pay the reader’s attention to the term "half-move”, which is frequently used in chess programming. By a half-move we will understand one move of White or one move of Black, in our case a half-move corresponds to the one-level down transition along the tree. While "complete move", or simply a move, means two moves - a move of White and the answer of Black, that corresponds to the two-level down transition.

Let's continue to grow the tree, drawing down branches from the initial position so that under the zero level there will be the first, under the first - the second, under the second – the thi …. Here the first trouble is waiting for us.

Trouble № 1.

The tree is being constructed wonderfully up to the second level. We have one position at the zero level. At the first level there are 1 х 20 = 20 positions. At the second level there are 20 х 20 = 400. And how many positions are to be constructed at the third level? The naive reader will tell: that’s very simple 400 х 20 = 8000, and … will be wrong. Let’s return on the level № 2 for explanations. And why, in fact, are we so sure, that there are 400 chess positions on it? You see, we have accepted the statement (which is actually true), that Black has 20 variants of answers after any first move of White, without any check. To prove strictly such a statement we should successively, leaf by leaf, draw all the 400 positions - and there is no other way! And at the third level we should draw not 8000 positions, but - 8902! The matter is that the number of possible moves of White in each of the 400 positions of the second level is different. So, we have accordingly for White – 32, 28 and 19 possible moves in three at random taken positions of the second level.

Diagram 2. There are 32 possible moves of White.

 

Diagram 3. There are 28 possible moves of White.

 

Diagram 4. There are 19 possible moves of White

One cannot manage here with simple multiplication: one needs several tens of hours to enumerate successively all the possible positions in order to count up precisely the number of positions at the third level. For this reason "tree" is usually called “searching-tree”. (Probably, the most exact name for it should be “tree of positions”).

The problem consists in impossibility to calculate with the help of some simple formula the quantity of positions in the tree starting from the third level. The exact number of positions at any level of the tree can be obtained only by means of complete enumeration of possible moves of white and black pieces, starting from the initial position (from zero level). In other words, it is necessary to construct the tree successively, level by level, including all its branches and leaves. This task is obviously beyond human's power. The modern computers can be of little help as well. It will take 7 hours to construct a tree of a maximum - 7 levels, using a usual personal computer. Moreover, there are 8902 leaves on the third level, 197281 on the fourth and 4865351 on the fifth. It is also necessary to mention that the computer builds up a three-level tree in 2 seconds, five-level - in 2 minutes and six-level - in 1 hour.

As it unexpectedly was found out, our harmonious approach to the growing of the tree on a sheet of a paper (or with the help of a computer in its computer memory) turns out to be almost senseless. The tree grows too fast! None computer will ever construct a tree, which will correspond to the 50th move of the black - a hundred-level! tree. There are no such computer capacities (computer memory and speed). We will illustrate this by the approximate time of calculation of positions starting from the sixth level on a computer like "Pentium-III".

6 ~ 1 hour

7 ~ 24 hours

8 ~ further the process becomes so time-consuming, that weeks of non-stop computer calculations are required.                                                              

       To tell the truth, we understand, that the tree exists irrespective of our inability to construct it. A human being, unlike a computer, can continue the construction of the tree mentally, both broadening it and extending it downwards as far as the imagination will suffice.     

 В дальнейшем число возможных ходов белых или черных в какой-либо позиции будем называть «подвижностью». Понятно, что в позициях, где ход белых (четные уровни дерева), речь может идти только о подвижности белых фигур. Соответственно в позициях, где ход черных (нечетные уровни), можно говорить о подвижности черных фигур.  Наверное, этот термин не очень удачен для такого понятия как шахматное дерево, но в последующих рассуждениях, когда начнется собственно игра в шахматы, этот термин  нам очень пригодится. Ясно, что подвижность в любой позиции - это есть количество ветвей в дереве,  которое произрастает из этой позиции (листа).

Henceforth we will call the number of possible moves of White or Black in any position as "mobility". It is quite clear, that in those positions, where White are to move (even levels of the tree), we can speak only about the mobility of white pieces. Accordingly, in positions, where Black are to move (odd levels), it is possible to speak about the mobility of black pieces. Probably, this term is not appropriate for such a concept as a chess tree, but it will be very useful for us in the next discussions, when we will pass to the real game of chess. It’s clear, that the mobility in any position corresponds to the number of branches of the tree, which grow from this position (or leaf).

Tree of positions – searching-tree.

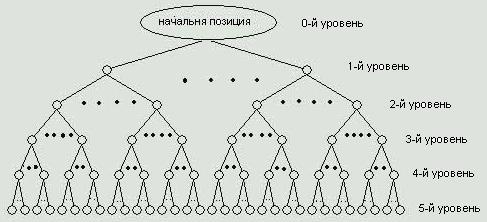
Figure 2. The tree grows down from an initial position to infinity

In spite of the fact that we can’t describe a tree precisely up to the level which includes the majority of human games (160th level - 80 moves), because of its enormous sizes, nevertheless, using simple logic methods, we can fix some integral properties of the tree:

Property 1 - there are identical positions in the tree. Really, already at the third level among 8902 positions there are some initial positions. (One of the initial positions can appear at the third level of the tree after the following moves 1. Кg1 - f3 Kg8 - f6. 2. Kf3 - g1 Kf6 - g8). Reasoning in the same way, it is easy to come to a conclusion, that there are also various sets of identical "not initial" positions in the tree.

Property 2 - the tree is infinite, that follows directly from Property 1 and the condition accepted by us, that we ignore chess laws of "triple repetition of a position” and of “fifty moves”. Indeed, from any initial position of the third level it is possible to construct absolutely the same tree, as the one, starting from the initial position of the first level. Thus, at levels 0, 3, 7, 11, 15 and further to infinity there are initial positions.  

Property 3 - there are deadlock branches in the tree. Really, from those positions of the tree where a checkmate or a stalemate is fixed, branches do not grow. (Using the accepted terminology, it is possible to say, that there is zero mobility in such positions).

Certainly, all the properties of the tree can not be reduced to the three mentioned, but we will return to these three in the next lectures.

In conclusion of the first lecture, it is necessary to pay special attention of the readers to the fact that the tree contains all the games which were ever played before, as well as the games which will be played (the tree includes all existing electronic bases of chess games. The tree contains all the chess information which is interesting for the chess players. The answers to all questions connected with estimation of this or that position are ciphered in this tree. Within the tree there is the answer to an eternal question – “White begins and …?”.